Heaps is written on this weblog about “Poststratification”. Andrew addresses it formally with a “Mister“. However once I realized it from Alan Zaslavsky’s course it was casually simply “Poststratification”. On the time it sounded to me like injury management after we forgot to stratify.

- “Stratification” = divide the inhabitants into strata (i.e. teams) based mostly on some variables X. To not reinforce social hierarchies, however to intention for representativeness. If we stratify earlier than choosing the pattern, we will take a pattern in every stratum for representativeness.
- “Publish” = divide the inhabitants into strata solely after the pattern is already chosen.
Fancy graphics from a DOL video I labored on:

How can Poststratification assist ?
Suppose we need to estimate E[Y], the inhabitants imply. However we solely have Y within the survey pattern. For instance, suppose Y is voting Republican. We will use the pattern imply, ybar = Ehat[Y | sample] (I don’t know LaTeX on this weblog).
However our pattern imply is conditional on being sampled. And what if survey-takers are roughly Republican than the inhabitants ? As Joe Blitzstein teaches us: “Conditioning is the soul of statistics.” Conditioning on being sampled may bias our estimate. However possibly extra conditioning may also in some way assist us ?! Joe taught me to strive conditioning at any time when I get caught.

If now we have inhabitants information on X, e.g. racial group, then we will estimate Republican vote share conditional on racial group E[Y|X] and combination in keeping with the recognized distribution of racial teams, invoking the regulation of complete expectation (Joe’s favourite): E[Y] = E[E[Y|X]]. So if our pattern has the mistaken distribution of racial teams, no less than we repair that with some calibration. Changing “E” with estimates “Ehat”, poststratification estimates E[Y] with E[Ehat[Y | X, sample]].
When our estimate of E[Y|X] is the pattern imply of Y for people with that X, the mixture estimate is classical poststratification, yhat_PS. When our estimate of E[Y|X] is predicated on a mannequin that regularizes throughout X, the mixture estimate is Multilevel Regression (“Mister“) and Poststratification, yhat_MRP. Gelman 2007 exhibits how yhat_MRP is a shrinkage of yhat_PS in direction of ybar.
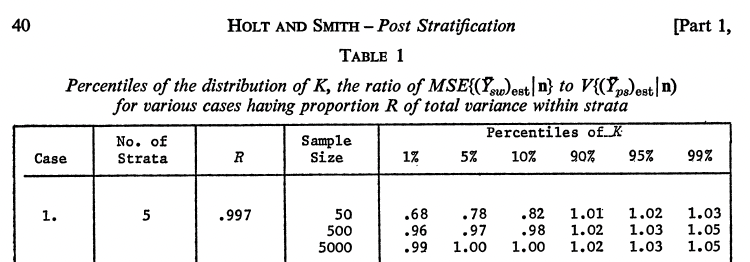
Which estimate is greatest for estimating E[Y] ? ybar, yhat_PS, or yhat_MRP ?
As Kuh et al 2023 write:
it isn’t particular person predictions that must be good, however quite the aggregations of those particular person estimates.
A parallel strategy is thru simulation research—for larger realism, these can usually be constructed utilizing subsamples of precise surveys—in addition to theoretical research of the bias and variance of poststratified estimates with reasonable pattern sizes.