In at the moment’s data-driven world, environment friendly geospatial indexing is essential for purposes starting from ride-sharing and logistics to environmental monitoring and catastrophe response. Uber’s H3, a strong open-source spatial indexing system, offers a novel hexagonal grid-based resolution that allows seamless geospatial evaluation and quick question execution. In contrast to conventional rectangular grid techniques, H3’s hierarchical hexagonal tiling ensures uniform spatial protection, higher adjacency properties, and lowered distortion. This information explores H3’s core ideas, set up, performance, use instances, and greatest practices to assist builders and information scientists leverage its full potential.
Studying Targets
- Perceive the basics of Uber’s H3 spatial indexing system and its benefits over conventional grid techniques.
- Discover ways to set up and arrange H3 for geospatial purposes in Python, JavaScript, and different languages.
- Discover H3’s hierarchical hexagonal grid construction and its advantages for spatial accuracy and indexing.
- Achieve hands-on expertise with core H3 features like neighbor lookup, polygon indexing, and distance calculations.
- Uncover real-world purposes of H3, together with machine studying, catastrophe response, and environmental monitoring.
This text was printed as part of the Knowledge Science Blogathon.
What’s Uber H3?
Uber H3 is an open-source, hexagonal hierarchical spatial indexing system developed by Uber. It’s designed to effectively partition and index geographic area, enabling superior geospatial evaluation, quick queries, and seamless visualization. In contrast to conventional grid techniques that use sq. or rectangular tiles, H3 makes use of hexagons, which give superior spatial relationships, higher adjacency properties, and decrease distortion when representing the Earth’s floor.
Why Uber Developed H3?
Uber developed H3 to resolve key challenges in geospatial computing, notably in ride-sharing, logistics, and location-based providers. Conventional approaches primarily based on latitude-longitude coordinates, rectangular grids, or QuadTrees usually undergo from inconsistencies in decision, inefficient spatial queries, and poor illustration of real-world spatial relationships. H3 addresses these limitations by:
- Offering a uniform, hierarchical hexagonal grid that permits for seamless scalability throughout totally different resolutions.
- Enabling quick nearest-neighbour lookups and environment friendly spatial indexing for ride-demand forecasting, routing, and provide distribution.
- Supporting spatial queries and geospatial clustering with excessive accuracy and minimal computational overhead.
Right this moment, H3 is broadly utilized in purposes past Uber, together with environmental monitoring, geospatial analytics, and geographic data techniques (GIS).
What’s Spatial Indexing?
Spatial indexing is a method used to construction and manage geospatial information effectively, permitting for quick spatial queries and improved information retrieval efficiency. It’s essential for duties akin to:
- Nearest neighbor search
- Geospatial clustering
- Environment friendly geospatial joins
- Area-based filtering
H3 enhances spatial indexing by utilizing a hexagonal grid system, which improves spatial accuracy, offers higher adjacency properties, and reduces distortions present in conventional grid-based techniques.
Set up Information (Python, JavaScript, Go, C, and so forth.)
Setting Up H3 in a Growth Setting
Allow us to now arrange H3 in a growth setting beneath:
# Create a digital setting
python -m venv h3_env
supply h3_env/bin/activate # Linux/macOS
h3_envScriptsactivate # Home windows
# Set up dependencies
pip set up h3 geopandas matplotlibKnowledge Construction and Hierarchical Indexing
Under we are going to perceive information construction and hierarchical indexing intimately:
Hexagonal Grid System
H3’s hexagonal grid partitions Earth into 122 base cells (decision 0), comprising 110 hexagons and 12 pentagons to approximate spherical geometry. Every cell undergoes hierarchical subdivision utilizing aperture 7 partitioning, the place each mum or dad hexagon accommodates 7 little one cells on the subsequent decision degree. This creates 16 decision ranges (0-15) with exponentially lowering cell sizes:
| Decision | Avg Edge Size (km) | Avg Space (km²) | Cell Depend per Mother or father |
|---|---|---|---|
| 0 | 1,107.712 | 4,250,546 | – |
| 5 | 8.544 | 252.903 | 16,807 |
| 9 | 0.174 | 0.105 | 40,353,607 |
| 15 | 0.0005 | 0.0000009 | 7^15 ≈ 4.7e12 |
The code beneath demonstrates H3’s hierarchical hexagonal grid system :
import folium
import h3
base_cell="8001fffffffffff" # Decision 0 pentagon
kids = h3.cell_to_children(base_cell, res=1)
# Create a map centered on the middle of the bottom hexagon
base_center = h3.cell_to_latlng(base_cell)
GeoSpatialMap = folium.Map(location=[base_center[0], base_center[1]], zoom_start=9)
# Operate to get hexagon boundaries
def get_hexagon_bounds(h3_address):
boundaries = h3.cell_to_boundary(h3_address)
# Folium expects coordinates in [lat, lon] format
return [[lat, lng] for lat, lng in boundaries]
# Add base hexagon
folium.Polygon(
areas=get_hexagon_bounds(base_cell),
shade="purple",
fill=True,
weight=2,
popup=f'Base: {base_cell}'
).add_to(GeoSpatialMap)
# Add kids hexagons
for little one in kids:
folium.Polygon(
areas=get_hexagon_bounds(little one),
shade="blue",
fill=True,
weight=1,
popup=f'Baby: {little one}'
).add_to(GeoSpatialMap)
GeoSpatialMap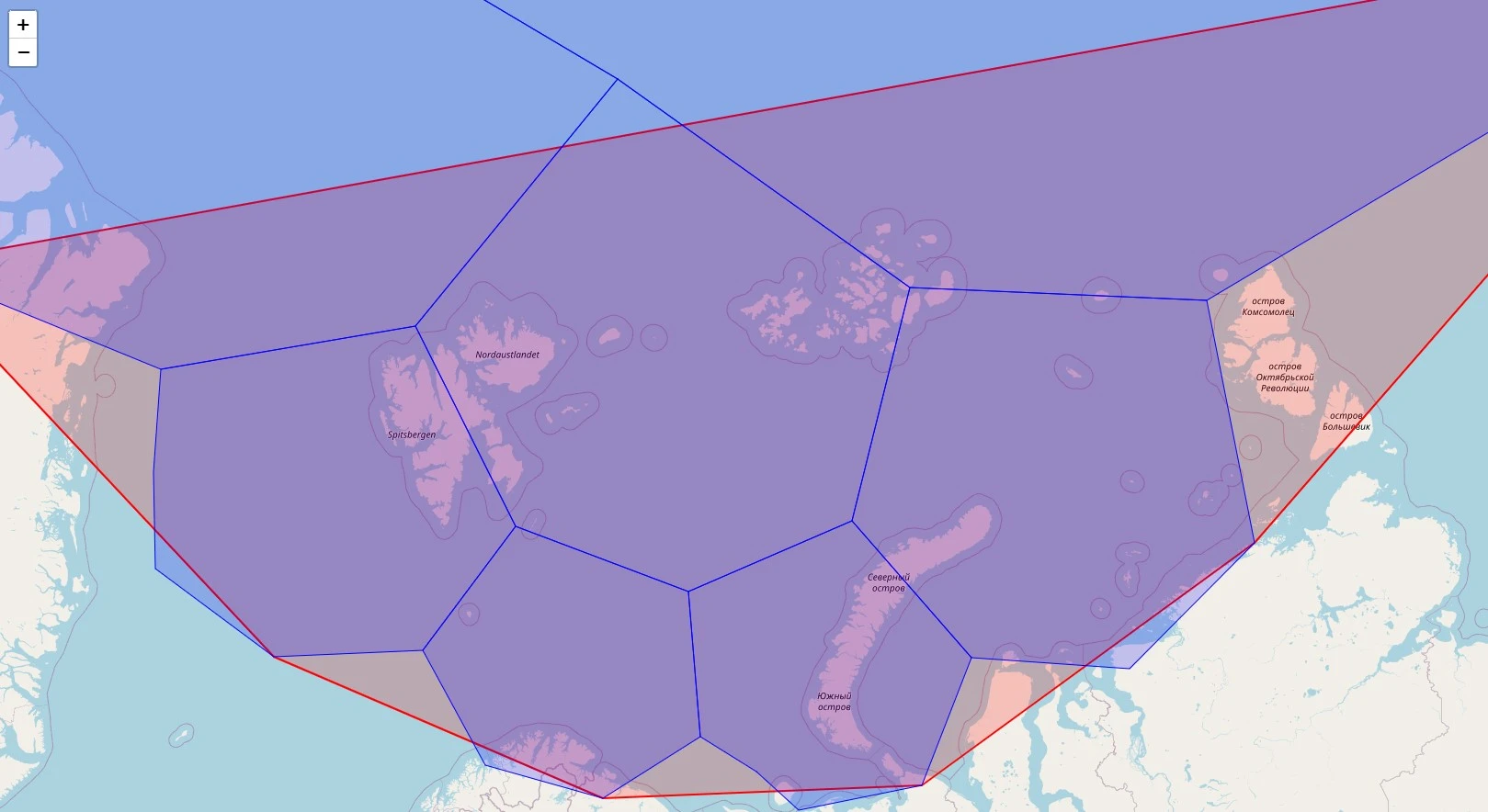
Decision Ranges and Hierarchical Indexing
The hierarchical indexing construction allows multi-resolution evaluation by parent-child relationships. H3 helps hierarchical decision ranges (from 0 to fifteen), permitting information to be listed at totally different granularities.
The given code beneath exhibits this relationship:
delhi_cell = h3.latlng_to_cell(28.6139, 77.2090, 9) # New Delhi coordinates
# Traverse hierarchy upwards
mum or dad = h3.cell_to_parent(delhi_cell, res=8)
print(f"Mother or father at res 8: {mum or dad}")
# Traverse hierarchy downwards
kids = h3.cell_to_children(mum or dad, res=9)
print(f"Incorporates {len(kids)} kids")
# Create a brand new map centered on New Delhi
delhi_map = folium.Map(location=[28.6139, 77.2090], zoom_start=15)
# Add the mum or dad hexagon (decision 8)
folium.Polygon(
areas=get_hexagon_bounds(mum or dad),
shade="purple",
fill=True,
weight=2,
popup=f'Mother or father: {mum or dad}'
).add_to(delhi_map)
# Add all kids hexagons (decision 9)
for child_cell in kids:
shade="yellow" if child_cell == delhi_cell else 'blue'
folium.Polygon(
areas=get_hexagon_bounds(child_cell),
shade=shade,
fill=True,
weight=1,
popup=f'Baby: {child_cell}'
).add_to(delhi_map)
delhi_map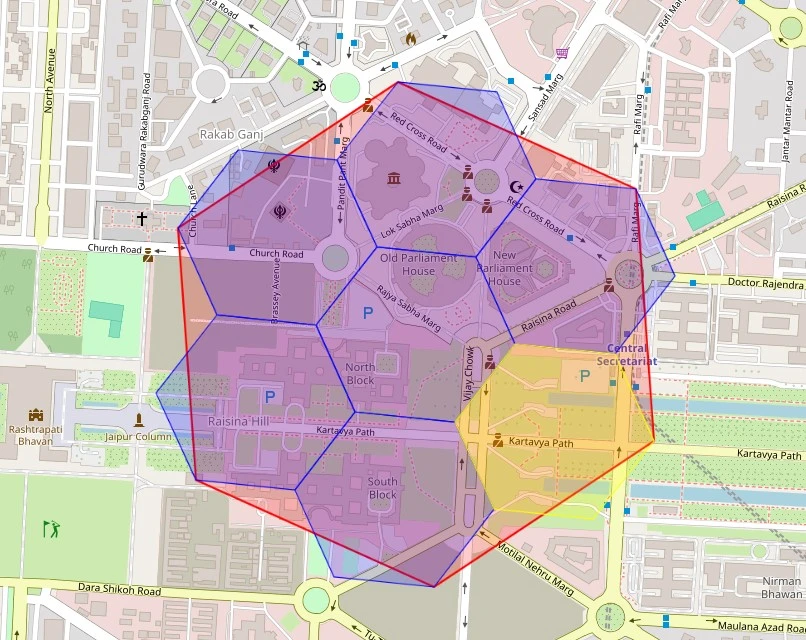
H3 Index Encoding
The H3 index encodes geospatial information right into a 64-bit unsigned integer (generally represented as a 15-character hexadecimal string like ‘89283082837ffff’). H3 indexes have the next structure:
| 4 bits | 3 bits | 7 bits | 45 bits |
|---|---|---|---|
| Mode and Decision | Reserved | Base Cell | Baby digits |
We are able to perceive the encoding course of by the next code beneath:
import h3
# Convert coordinates to H3 index (decision 9)
lat, lng = 37.7749, -122.4194 # San Francisco
h3_index = h3.latlng_to_cell(lat, lng, 9)
print(h3_index) # '89283082803ffff'
# Deconstruct index elements
## Get the decision
decision = h3.get_resolution(h3_index)
print(f"Decision: {decision}")
# Output: 9
# Get the bottom cell quantity
base_cell = h3.get_base_cell_number(h3_index)
print(f"Base cell: {base_cell}")
# Output: 20
# Verify if its a pentagon
is_pentagon = h3.is_pentagon(h3_index)
print(f"Is pentagon: {is_pentagon}")
# Output: False
# Get the icosahedron face
face = h3.get_icosahedron_faces(h3_index)
print(f"Face quantity: {face}")
# Output: [7]
# Get the kid cells
child_cells = h3.cell_to_children(h3.cell_to_parent(h3_index, 8), 9)
print(f"little one cells: {child_cells}")
# Output: ['89283082803ffff', '89283082807ffff', '8928308280bffff', '8928308280fffff',
# '89283082813ffff', '89283082817ffff', '8928308281bffff']Core Features
Other than the Hierarchical Indexing, among the different Core features of H3 are as follows:
- Neighbor Lookup & Traversal
- Polygon to H3 Indexing
- H3 Grid Distance and Ok-Ring
Neighbor Lookup andTraversal
Neighbor lookup traversal refers to figuring out and navigating between adjoining cells in Uber’s H3 hexagonal grid system. This permits spatial queries like “discover all cells inside a radius of ok steps” from a goal cell. This idea might be understood from the code beneath:
import h3
# Outline latitude, longitude for Kolkata
lat, lng = 22.5744, 88.3629
decision = 9
h3_index = h3.latlng_to_cell(lat, lng, decision)
print(h3_index) # e.g., '89283082837ffff'
# Discover all neighbors inside 1 grid step
neighbors = h3.grid_disk(h3_index, ok=1)
print(len(neighbors)) # 7 (6 neighbors + the unique cell)
# Verify edge adjacency
is_neighbor = h3.are_neighbor_cells(h3_index, neighbors[0])
print(is_neighbor) # True or FalseTo generate the visualization of this we are able to merely use the code given beneath:
import h3
import folium
# Outline latitude, longitude for Kolkata
lat, lng = 22.5744, 88.3629
decision = 9 # H3 decision
# Convert lat/lng to H3 index
h3_index = h3.latlng_to_cell(lat, lng, decision)
# Get neighboring hexagons
neighbors = h3.grid_disk(h3_index, ok=1)
# Initialize map centered on the given location
m = folium.Map(location=[lat, lng], zoom_start=12)
# Operate so as to add hexagons to the map
def add_hexagon(h3_index, shade):
""" Provides an H3 hexagon to the folium map """
boundary = h3.cell_to_boundary(h3_index)
# Convert to [lat, lng] format for folium
boundary = [[lat, lng] for lat, lng in boundary]
folium.Polygon(
areas=boundary,
shade=shade,
fill=True,
fill_color=shade,
fill_opacity=0.5
).add_to(m)
# Add central hexagon in purple
add_hexagon(h3_index, "purple")
# Add neighbor hexagons in blue
for neighbor in neighbors:
if neighbor != h3_index: # Keep away from recoloring the middle
add_hexagon(neighbor, "blue")
# Show the map
m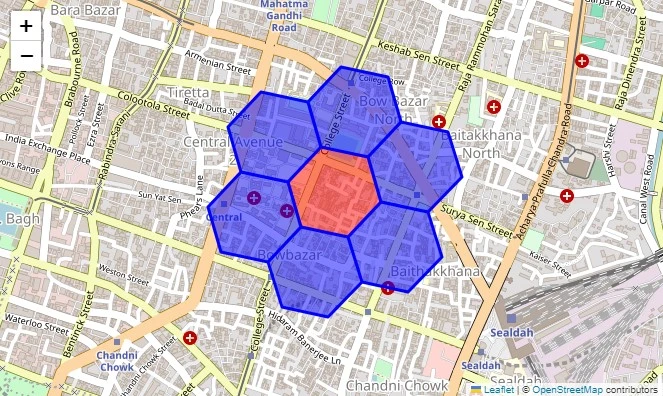
Use instances of Neighbor Lookup & Traversal are as follows:
- Journey Sharing: Discover accessible drivers inside a 5-minute drive radius.
- Spatial Aggregation: Calculate complete rainfall in cells inside 10 km of a flood zone.
- Machine Studying: Generate neighborhood options for demand prediction fashions.
Polygon to H3 Indexing
Changing a polygon to H3 indexes entails figuring out all hexagonal cells at a specified decision that totally or partially intersect with the polygon. That is essential for spatial operations like aggregating information inside geographic boundaries. This could possibly be understood from the given code beneath:
import h3
# Outline a polygon (e.g., San Francisco bounding field)
polygon_coords = h3.LatLngPoly(
[(37.708, -122.507), (37.708, -122.358), (37.832, -122.358), (37.832, -122.507)]
)
# Convert polygon to H3 cells (decision 9)
decision = 9
cells = h3.polygon_to_cells(polygon_coords, res=decision)
print(f"Whole cells: {len(cells)}")
# Output: ~ 1651To visualise this we are able to observe the given code beneath:
import h3
import folium
from h3 import LatLngPoly
# Outline a bounding polygon for Kolkata
kolkata_coords = LatLngPoly([
(22.4800, 88.2900), # Southwest corner
(22.4800, 88.4200), # Southeast corner
(22.5200, 88.4500), # East
(22.5700, 88.4500), # Northeast
(22.6200, 88.4200), # North
(22.6500, 88.3500), # Northwest
(22.6200, 88.2800), # West
(22.5500, 88.2500), # Southwest
(22.5000, 88.2700) # Return to starting area
])
# Add extra boundary coordinates for extra particular map
# Convert polygon to H3 cells
decision = 9
cells = h3.polygon_to_cells(kolkata_coords, res=decision)
# Create a Folium map centered round Kolkata
kolkata_map = folium.Map(location=[22.55, 88.35], zoom_start=12)
# Add every H3 cell as a polygon
for cell in cells:
boundaries = h3.cell_to_boundary(cell)
# Convert to [lat, lng] format for folium
boundaries = [[lat, lng] for lat, lng in boundaries]
folium.Polygon(
areas=boundaries,
shade="blue",
weight=1,
fill=True,
fill_opacity=0.4,
popup=cell
).add_to(kolkata_map)
# Present map
kolkata_map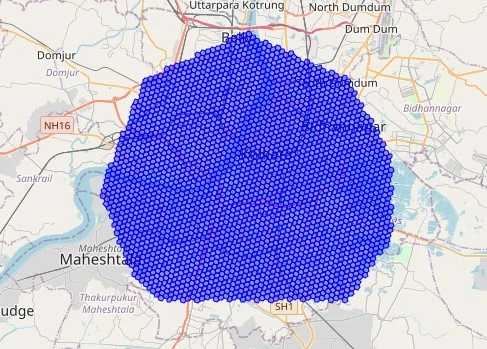
H3 Grid Distance and Ok-Ring
Grid distance measures the minimal variety of steps required to traverse from one H3 cell to a different, shifting by adjoining cells. In contrast to geographical distance, it’s a topological metric primarily based on hexagonal grid connectivity. And we must always needless to say increased resolutions yield smaller steps so the grid distance can be bigger.
import h3
from h3 import latlng_to_cell
# Outline two H3 cells at decision 9
cell_a = latlng_to_cell(37.7749, -122.4194, 9) # San Francisco
cell_b = latlng_to_cell(37.3382, -121.8863, 9) # San Jose
# Calculate grid distance
distance = h3.grid_distance(cell_a, cell_b)
print(f"Grid distance: {distance} steps")
# Output: Grid distance: 220 steps (approx)We are able to visualize this with the next given code:
import h3
import folium
from h3 import latlng_to_cell
from shapely.geometry import Polygon
# Operate to get H3 polygon boundary
def get_h3_polygon(h3_index):
boundary = h3.cell_to_boundary(h3_index)
return [(lat, lon) for lat, lon in boundary]
# Outline two H3 cells at decision 6
cell_a = latlng_to_cell(37.7749, -122.4194, 6) # San Francisco
cell_b = latlng_to_cell(37.3382, -121.8863, 6) # San Jose
# Get hexagon boundaries
polygon_a = get_h3_polygon(cell_a)
polygon_b = get_h3_polygon(cell_b)
# Compute grid distance
distance = h3.grid_distance(cell_a, cell_b)
# Create a folium map centered between the 2 areas
map_center = [(37.7749 + 37.3382) / 2, (-122.4194 + -121.8863) / 2]
m = folium.Map(location=map_center, zoom_start=9)
# Add H3 hexagons to the map
folium.Polygon(areas=polygon_a, shade="blue", fill=True, fill_opacity=0.4, popup="San Francisco (H3)").add_to(m)
folium.Polygon(areas=polygon_b, shade="purple", fill=True, fill_opacity=0.4, popup="San Jose (H3)").add_to(m)
# Add markers for the middle factors
folium.Marker([37.7749, -122.4194], popup="San Francisco").add_to(m)
folium.Marker([37.3382, -121.8863], popup="San Jose").add_to(m)
# Show distance
folium.Marker(map_center, popup=f"H3 Grid Distance: {distance} steps", icon=folium.Icon(shade="inexperienced")).add_to(m)
# Present the map
m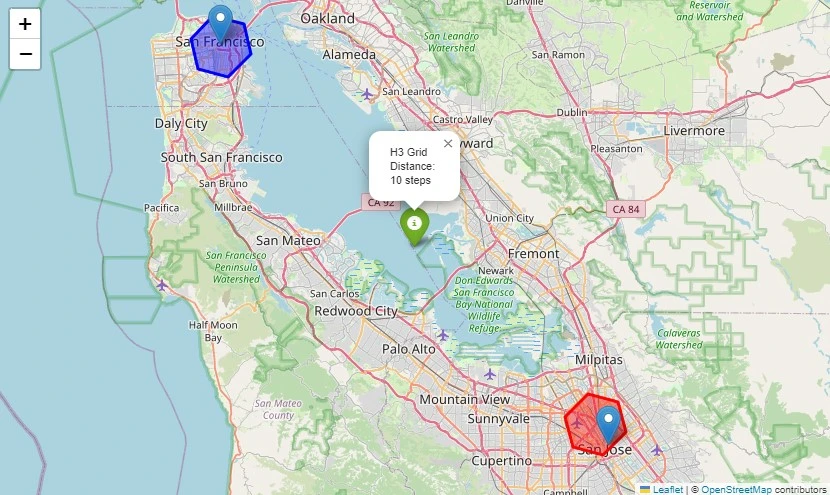
And Ok-Ring (or grid disk) in H3 refers to all hexagonal cells inside ok grid steps from a central cell. This consists of:
- The central cell itself (at step 0).
- Instant neighbors (step 1).
- Cells at progressively bigger distances as much as `ok` steps.
import h3
# Outline a central cell (San Francisco at decision 9)
central_cell = h3.latlng_to_cell(37.7749, -122.4194, 9)
ok = 2
# Generate Ok-Ring (cells inside 2 steps)
k_ring = h3.grid_disk(central_cell, ok)
print(f"Whole cells: {len(k_ring)}") # e.g., 19 cells This may be visualized from the plot given beneath:
import h3
import matplotlib.pyplot as plt
from shapely.geometry import Polygon
import geopandas as gpd
# Outline central level (latitude, longitude) for San Francisco [1]
lat, lng = 37.7749, -122.4194
decision = 9 # Select decision (e.g., 9) [1]
# Acquire central H3 cell index for the given level [1]
center_h3 = h3.latlng_to_cell(lat, lng, decision)
print("Central H3 cell:", center_h3) # Instance output: '89283082837ffff'
# Outline ok worth (variety of grid steps) for the k-ring [1]
ok = 2
# Generate k-ring of cells: all cells inside ok grid steps of centerH3 [1]
k_ring_cells = h3.grid_disk(center_h3, ok)
print("Whole k-ring cells:", len(k_ring_cells))
# For the standard hexagon (non-pentagon), ok=2 sometimes returns 19 cells:
# 1 (central cell) + 6 (neighbors at distance 1) + 12 (neighbors at distance 2)
# Convert every H3 cell right into a Shapely polygon for visualization [1][6]
polygons = []
for cell in k_ring_cells:
# Get the cell boundary as an inventory of (lat, lng) pairs; geo_json=True returns in [lat, lng]
boundary = h3.cell_to_boundary(cell)
# Swap to (lng, lat) as a result of Shapely expects (x, y)
poly = Polygon([(lng, lat) for lat, lng in boundary])
polygons.append(poly)
# Create a GeoDataFrame for plotting the hexagonal cells [2]
gdf = gpd.GeoDataFrame({'h3_index': checklist(k_ring_cells)}, geometry=polygons)
# Plot the boundaries of the k-ring cells utilizing Matplotlib [2][6]
fig, ax = plt.subplots(figsize=(8, 8))
gdf.boundary.plot(ax=ax, shade="blue", lw=1)
# Spotlight the central cell by plotting its boundary in purple [1]
central_boundary = h3.cell_to_boundary(center_h3)
central_poly = Polygon([(lng, lat) for lat, lng in central_boundary])
gpd.GeoSeries([central_poly]).boundary.plot(ax=ax, shade="purple", lw=2)
# Set plot labels and title for clear visualization
ax.set_title("H3 Ok-Ring Visualization (ok = 2)")
ax.set_xlabel("Longitude")
ax.set_ylabel("Latitude")
plt.present()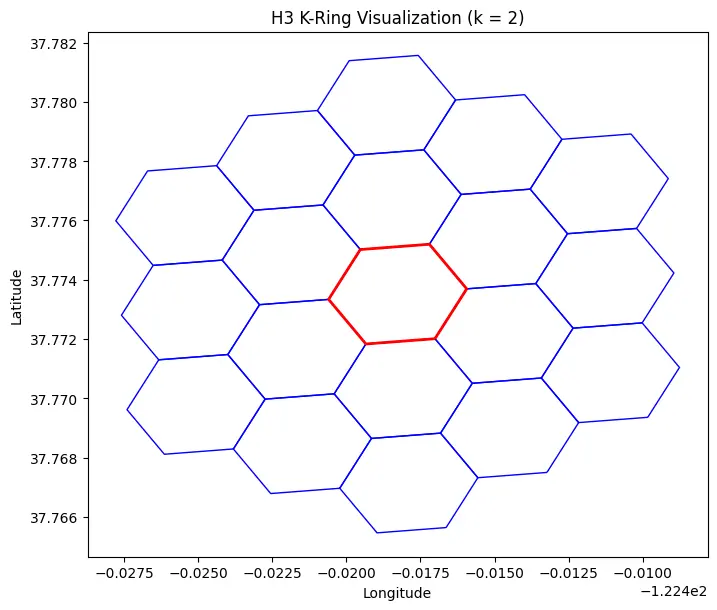
Use Instances
Whereas the use instances of H3 are solely restricted to at least one’s creativity, listed here are few examples of it :
Environment friendly Geo-Spatial Queries
H3 excels at optimizing location-based queries, akin to counting factors of curiosity (POIs) inside dynamic geographic boundaries.
On this use case, we exhibit how H3 might be utilized to investigate and visualize trip pickup density in San Francisco utilizing Python. To simulate real-world trip information, we generate random GPS coordinates centered round San Francisco. We additionally assign every trip a random timestamp inside the previous week to create a sensible dataset. Every trip’s latitude and longitude are transformed into an H3 index at decision 10, a fine-grained hexagonal grid that helps in spatial aggregation. To investigate native trip pickup density, we choose a goal H3 cell and retrieve all close by cells inside two hexagonal rings utilizing h3.grid_disk. To visualise the spatial distribution of pickups, we overlay the H3 hexagons onto a Folium map.
Code Implementation
The execution code is given beneath:
import pandas as pd
import h3
import folium
import matplotlib.pyplot as plt
import numpy as np
from datetime import datetime, timedelta
import random
# Create pattern GPS information round San Francisco
# Middle coordinates for San Francisco
center_lat, center_lng = 37.7749, -122.4194
# Generate artificial trip information
num_rides = 1000
np.random.seed(42) # For reproducibility
# Generate random coordinates round San Francisco
lats = np.random.regular(center_lat, 0.02, num_rides) # Regular distribution round middle
lngs = np.random.regular(center_lng, 0.02, num_rides)
# Generate timestamps for the previous week
start_time = datetime.now() - timedelta(days=7)
timestamps = [start_time + timedelta(minutes=random.randint(0, 10080)) for _ in range(num_rides)]
timestamp_strs = [ts.strftime('%Y-%m-%d %H:%M:%S') for ts in timestamps]
# Create DataFrame
rides = pd.DataFrame({
'lat': lats,
'lng': lngs,
'timestamp': timestamp_strs
})
# Convert coordinates to H3 indexes (decision 10)
rides["h3"] = rides.apply(
lambda row: h3.latlng_to_cell(row["lat"], row["lng"], 10), axis=1
)
# Depend pickups per cell
pickup_counts = rides["h3"].value_counts().reset_index()
pickup_counts.columns = ["h3", "counts"]
# Question pickups inside a selected cell and its neighbors
target_cell = h3.latlng_to_cell(37.7749, -122.4194, 10)
neighbors = h3.grid_disk(target_cell, ok=2)
local_pickups = pickup_counts[pickup_counts["h3"].isin(neighbors)]
# Visualize the spatial question outcomes
map_center = h3.cell_to_latlng(target_cell)
m = folium.Map(location=map_center, zoom_start=15)
# Operate to get hexagon boundaries
def get_hexagon_bounds(h3_address):
boundaries = h3.cell_to_boundary(h3_address)
return [[lat, lng] for lat, lng in boundaries]
# Add goal cell
folium.Polygon(
areas=get_hexagon_bounds(target_cell),
shade="purple",
fill=True,
weight=2,
popup=f'Goal Cell: {target_cell}'
).add_to(m)
# Shade scale for counts
max_count = local_pickups["counts"].max()
min_count = local_pickups["counts"].min()
# Add neighbor cells with shade depth primarily based on pickup counts
for _, row in local_pickups.iterrows():
if row["h3"] != target_cell:
# Calculate shade depth primarily based on depend
depth = (row["counts"] - min_count) / (max_count - min_count) if max_count > min_count else 0.5
shade = f'#{int(255*(1-intensity)):02x}{int(200*(1-intensity)):02x}ff'
folium.Polygon(
areas=get_hexagon_bounds(row["h3"]),
shade=shade,
fill=True,
fill_opacity=0.7,
weight=1,
popup=f'Cell: {row["h3"]}
Pickups: {row["counts"]}'
).add_to(m)
# Create a heatmap visualization with matplotlib
plt.determine(figsize=(12, 8))
plt.title("H3 Grid Heatmap of Journey Pickups")
# Create a scatter plot for cells, dimension primarily based on pickup counts
for idx, row in local_pickups.iterrows():
middle = h3.cell_to_latlng(row["h3"])
plt.scatter(middle[1], middle[0], s=row["counts"]/2,
c=row["counts"], cmap='viridis', alpha=0.7)
plt.colorbar(label="Variety of Pickups")
plt.xlabel('Longitude')
plt.ylabel('Latitude')
plt.grid(True)
# Show each visualizations
m # Show the folium map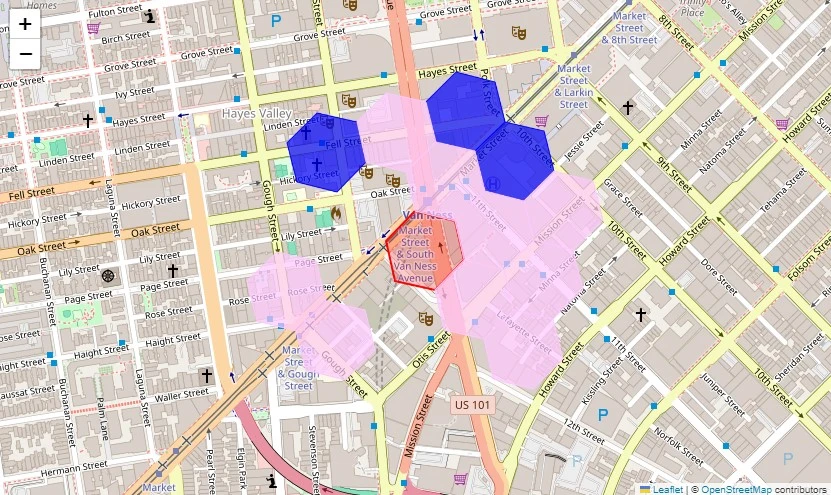
The above instance highlights how H3 might be leveraged for spatial evaluation in city mobility. By changing uncooked GPS coordinates right into a hexagonal grid, we are able to effectively analyze trip density, detect hotspots, and visualize information in an insightful method. H3’s flexibility in dealing with totally different resolutions makes it a worthwhile instrument for geospatial analytics in ride-sharing, logistics, and concrete planning purposes.
Combining H3 with Machine Studying
H3 has been mixed with Machine Studying to resolve many actual world issues. Uber lowered ETA prediction errors by 22% utilizing H3-based ML fashions whereas Toulouse, France, used H3 + ML to optimize bike lane placement, growing ridership by 18%.
On this use case, we exhibit how H3 might be utilized to investigate and predict visitors congestion in San Francisco utilizing historic GPS trip information and machine studying methods. To simulate real-world visitors circumstances, we generate random GPS coordinates centered round San Francisco. Every trip is assigned a random timestamp inside the previous week, together with a randomly generated velocity worth. Every trip’s latitude and longitude are transformed into an H3 index at decision 10, enabling spatial aggregation and evaluation. We extract options from a pattern cell and its neighboring cells inside two hexagonal rings to investigate native visitors circumstances. To foretell visitors congestion, we use an LSTM-based deep studying mannequin. The mannequin is designed to course of historic visitors information and predict congestion chances. Utilizing the educated mannequin, we are able to predict the chance of congestion for a given cell.
Code Implementation
The execution code is given beneath :
import h3
import pandas as pd
import numpy as np
from datetime import datetime, timedelta
import random
import tensorflow as tf
from tensorflow.keras.layers import LSTM, Conv1D, Dense
# Create pattern GPS information round San Francisco
center_lat, center_lng = 37.7749, -122.4194
num_rides = 1000
np.random.seed(42) # For reproducibility
# Generate random coordinates round San Francisco
lats = np.random.regular(center_lat, 0.02, num_rides)
lngs = np.random.regular(center_lng, 0.02, num_rides)
# Generate timestamps for the previous week
start_time = datetime.now() - timedelta(days=7)
timestamps = [start_time + timedelta(minutes=random.randint(0, 10080)) for _ in range(num_rides)]
timestamp_strs = [ts.strftime('%Y-%m-%d %H:%M:%S') for ts in timestamps]
# Generate random velocity information
speeds = np.random.uniform(5, 60, num_rides) # Velocity in km/h
# Create DataFrame
gps_data = pd.DataFrame({
'lat': lats,
'lng': lngs,
'timestamp': timestamp_strs,
'velocity': speeds
})
# Convert coordinates to H3 indexes (decision 10)
gps_data["h3"] = gps_data.apply(
lambda row: h3.latlng_to_cell(row["lat"], row["lng"], 10), axis=1
)
# Convert timestamp string to datetime objects
gps_data["timestamp"] = pd.to_datetime(gps_data["timestamp"])
# Mixture velocity and depend per cell per 5-minute interval
agg_data = gps_data.groupby(["h3", pd.Grouper(key="timestamp", freq="5T")]).agg(
avg_speed=("velocity", "imply"),
vehicle_count=("h3", "depend")
).reset_index()
# Instance: Use a cell from our present dataset
sample_cell = gps_data["h3"].iloc[0]
neighbors = h3.grid_disk(sample_cell, 2)
def get_kring_features(cell, ok=2):
neighbors = h3.grid_disk(cell, ok)
return {f"neighbor_{i}": neighbor for i, neighbor in enumerate(neighbors)}
# Placeholder perform for characteristic extraction
def fetch_features(neighbors, agg_data):
# In an actual implementation, this is able to fetch historic information for the neighbors
# That is only a simplified instance that returns random information
return np.random.rand(1, 6, len(neighbors)) # 1 pattern, 6 timesteps, options per neighbor
# Outline a skeleton mannequin structure
def create_model(input_shape):
mannequin = tf.keras.Sequential([
LSTM(64, return_sequences=True, input_shape=input_shape),
LSTM(32),
Dense(16, activation='relu'),
Dense(1, activation='sigmoid')
])
mannequin.compile(optimizer="adam", loss="binary_crossentropy", metrics=['accuracy'])
return mannequin
# Prediction perform (would use a educated mannequin in apply)
def predict_congestion(cell, mannequin, agg_data):
# Fetch neighbor cells
neighbors = h3.grid_disk(cell, ok=2)
# Get historic information for neighbors
options = fetch_features(neighbors, agg_data)
# Predict
return mannequin.predict(options)[0][0]
# Create a skeleton mannequin (not educated)
input_shape = (6, 19) # 6 time steps, 19 options (for ok=2 neighbors)
mannequin = create_model(input_shape)
# Print details about what would occur in an actual prediction
print(f"Pattern cell: {sample_cell}")
print(f"Variety of neighboring cells (ok=2): {len(neighbors)}")
print("Mannequin abstract:")
mannequin.abstract()
# In apply, you'll practice the mannequin earlier than utilizing it for predictions
# This may simply present what a prediction name would seem like:
congestion_prob = predict_congestion(sample_cell, mannequin, agg_data)
print(f"Congestion chance: {congestion_prob:.2%}")
# instance output- Congestion Chance: 49.09%This instance demonstrates how H3 might be leveraged for spatial evaluation and visitors prediction. By changing GPS information into hexagonal grids, we are able to effectively analyze visitors patterns, extract significant insights from neighboring areas, and use deep studying to foretell congestion in actual time. This method might be utilized to good metropolis planning, ride-sharing optimizations, and clever visitors administration techniques.
Catastrophe Response and Environmental Monitoring
Flood occasions signify one of the frequent pure disasters requiring rapid response and useful resource allocation. H3 can considerably enhance flood response efforts by integrating numerous information sources together with flood zone maps, inhabitants density, constructing infrastructure, and real-time water degree readings.
The next Python implementation demonstrates how to make use of H3 for flood threat evaluation by integrating flooded space information with constructing infrastructure data:
import h3
import folium
import pandas as pd
import numpy as np
from folium.plugins import MarkerCluster
# Create pattern buildings dataset
np.random.seed(42)
num_buildings = 50
# Create buildings round San Francisco
center_lat, center_lng = 37.7749, -122.4194
building_types = ['residential', 'commercial', 'hospital', 'school', 'government']
building_weights = [0.6, 0.2, 0.1, 0.07, 0.03] # Chance weights
# Generate constructing information
buildings_df = pd.DataFrame({
'lat': np.random.regular(center_lat, 0.005, num_buildings),
'lng': np.random.regular(center_lng, 0.005, num_buildings),
'sort': np.random.selection(building_types, dimension=num_buildings, p=building_weights),
'capability': np.random.randint(10, 1000, num_buildings)
})
# Add H3 index at decision 10
buildings_df['h3_index'] = buildings_df.apply(
lambda row: h3.latlng_to_cell(row['lat'], row['lng'], 10),
axis=1
)
# Create some flood cells (let's use some cells the place buildings are positioned)
# Taking a number of cells the place buildings are positioned to simulate a flood zone
flood_cells = set(buildings_df['h3_index'].pattern(10))
# Create a map centered on the common of our coordinates
center_lat = buildings_df['lat'].imply()
center_lng = buildings_df['lng'].imply()
flood_map = folium.Map(location=[center_lat, center_lng], zoom_start=16)
# Operate to get hexagon boundaries for folium
def get_hexagon_bounds(h3_address):
boundaries = h3.cell_to_boundary(h3_address)
# Folium expects coordinates in [lat, lng] format
return [[lat, lng] for lat, lng in boundaries]
# Add flood zone cells
for cell in flood_cells:
folium.Polygon(
areas=get_hexagon_bounds(cell),
shade="blue",
fill=True,
fill_opacity=0.4,
weight=2,
popup=f'Flood Cell: {cell}'
).add_to(flood_map)
# Add constructing markers
for idx, row in buildings_df.iterrows():
# Set shade primarily based on if constructing is affected
if row['h3_index'] in flood_cells:
shade="purple"
icon = 'warning' if row['type'] in ['hospital', 'school'] else 'info-sign'
prefix = 'glyphicon'
else:
shade="inexperienced"
icon = 'house'
prefix = 'glyphicon'
# Create marker with popup exhibiting constructing particulars
folium.Marker(
location=[row['lat'], row['lng']],
popup=f"Constructing Sort: {row['type']}
Capability: {row['capacity']}",
tooltip=f"{row['type']} (Capability: {row['capacity']})",
icon=folium.Icon(shade=shade, icon=icon, prefix=prefix)
).add_to(flood_map)
# Add a legend as an HTML aspect
legend_html=""'
Flood Affect Evaluation
Flood Zone
Secure Buildings
Affected Buildings
Crucial Services
'''
flood_map.get_root().html.add_child(folium.Factor(legend_html))
# Show the map
flood_map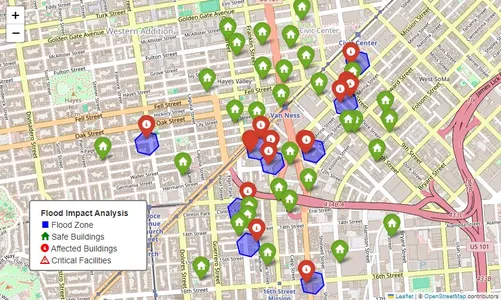
This code offers an environment friendly methodology for visualizing and analyzing flood impacts utilizing H3 spatial indexing and Folium mapping. By integrating spatial information clustering and interactive visualization, it enhances catastrophe response planning and concrete threat administration methods. This method might be prolonged to different geospatial challenges, akin to wildfire threat evaluation or transportation planning.
Strengths and Weaknesses of H3
The next desk offers an in depth evaluation of H3’s benefits and limitations primarily based on trade implementations and technical evaluations:
| Facet | Strengths | Weaknesses |
|---|---|---|
| Geometry Properties | Hexagonal cells present uniform distance metrics with equidistant neighbors. Higher approximation of circles than sq./rectangular grids. Minimizes each space and form distortion globally | Can not fully divide Earth into hexagons, requires 12 pentagon cells that create irregular adjacency patterns. Not a real equal-area system, regardless of aiming for “roughly equal-ish” areas |
| Hierarchical Construction | Effectively modifications precision (decision) ranges as wanted. Compact 64-bit addresses for all resolutions- Mother or father-child tree with no shared mother and father. | Hierarchical nesting between resolutions isn’t good. Tiny discontinuities (gaps/overlaps) can happen at adjoining scales. Problematic to be used instances requiring precise containment (e.g., parcel information) |
| Efficiency | H3-centric approaches might be as much as 90x cheaper than geometry-centric operations. Considerably enhances processing effectivity with giant dataset. Quick calculations between predictable cells in grid system | Processing giant areas at excessive resolutions requires vital computational sources. Commerce-off between precision and efficiency – increased resolutions eat extra sources. |
| Spatial Evaluation | Multi-resolution evaluation from neighborhood to regional scales. Standardized format for integrating heterogeneous information sources. Uniform adjacency relationships simplify neighborhood searches | Polygon protection is approximate with potential gaps at boundaries. Precision limitations depending on chosen decision degree. Particular dealing with required for polygon intersections |
| Implementation | Easy API with built-in utilities (geofence polyfill, hexagon compaction, GeoJSON output)- Nicely-suited for parallelized execution. Cell IDs can be utilized as columns in customary SQL features. | Dealing with pentagon cells requires specialised code. Adapting present workflows to H3 might be advanced. Knowledge high quality dependencies have an effect on evaluation accuracy |
| Functions | Optimized for: geospatial analytics, mobility evaluation, logistics, supply providers, telecoms, insurance coverage threat evaluation, and environmental monitoring. | Much less appropriate for purposes requiring precise boundary definitions. Might not be optimum for specialised cartographic functions. Can contain computational complexity for real-time purposes with restricted sources. |
Conclusion
Uber’s H3 spatial indexing system is a strong instrument for geospatial evaluation, providing a hexagonal grid construction that allows environment friendly spatial queries, multi-resolution evaluation, and seamless integration with fashionable information workflows. Its strengths lie in its uniform geometry, hierarchical design, and skill to deal with large-scale datasets with velocity and precision. From ride-sharing optimization to catastrophe response and environmental monitoring, H3 has confirmed its versatility throughout industries.
Nevertheless, like several expertise, H3 has limitations, akin to dealing with pentagon cells, approximating polygon boundaries, and computational calls for at excessive resolutions. By understanding its strengths and weaknesses, builders can leverage H3 successfully for purposes requiring scalable and correct geospatial insights.
As geospatial expertise evolves, H3’s open-source ecosystem will doubtless see additional enhancements, together with integration with machine studying fashions, real-time analytics, and 3D spatial indexing. H3 isn’t just a instrument however a basis for constructing smarter geospatial options in an more and more data-driven world.
Often Requested Questions
A. Go to the official H3 documentation or discover open-source examples on GitHub. Uber’s engineering weblog additionally offers insights into real-world purposes of H3.
A. Sure! With its quick indexing and neighbor lookup capabilities, H3 is extremely environment friendly for real-time geospatial purposes like stay visitors monitoring or catastrophe response coordination.
A. Sure! H3 is well-suited for machine studying purposes. By changing uncooked GPS information into hexagonal options (e.g., visitors density per cell), you’ll be able to combine spatial patterns into predictive fashions like demand forecasting or congestion prediction.
A. The core H3 library is written in C however has bindings for Python, JavaScript, Go, Java, and extra. This makes it versatile for integration into numerous geospatial workflows.
A. Whereas it’s inconceivable to tile a sphere completely with hexagons, H3 introduces 12 pentagon cells at every decision to shut gaps. To attenuate their affect on most datasets, the system strategically locations these pentagons over oceans or much less vital areas.
The media proven on this article will not be owned by Analytics Vidhya and is used on the Creator’s discretion.
Login to proceed studying and revel in expert-curated content material.




